İkinci Dereceden Bir Fonksiyonun Maksimum veya Minimum Değeri Nasıl Kolayca Bulunur?

Matematiğin temel taşlarından biri olan ikinci dereceden fonksiyonlar, günlük hayatımızda pek çok yerde karşımıza çıkmaktadır. Bu fonksiyonların maksimum veya minimum değerlerini bulmak ise, mühendislikten ekonomiye kadar pek çok alanda çözümlemek istediğimiz problemlerin anahtarı olmaktadır. Ancak, bu değerleri bulmak her zaman kolay olmamaktadır. Bunun için, ikinci dereceden bir fonksiyonun maksimum veya minimum değerini kolayca bulmak için bazı yöntemler geliştirilmiştir. Bu makalede, bu yöntemleri detaylı olarak ele alacağız ve ikinci dereceden bir fonksiyonun maksimum veya minimum değerini nasıl kolayca bulacağımızı öğreneceğiz.

İkinci Dereceden Bir Fonksiyonun Maksimum veya Minimum Değeri Nasıl Kolayca Bulunur?

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri bulmak, matematiksel analizde önemli bir konudur. Bu değerin bulunması, fonksiyonun grafiğinin maksimum veya minimum noktasını belirlemek için kullanılır.

Fonksiyonun Türevi

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri bulmak için, öncelikle fonksiyonun türevi alınmalıdır. Türev, fonksiyonun eğiminin değişimini gösterir. Türevi bulmak için, fonksiyonun birinci dereceden türevini alınır. Örneğin, f(x) = ax^2 + bx + c fonksiyonunun türevi, f'(x) = 2ax + b olacaktır.

Kritik Noktalar

Fonksiyonun türevi alınarak, kritik noktalar bulunur. Kritik noktalar, fonksiyonun eğiminin değiştiği noktalarıdır. Kritik noktaları bulmak için, türevi eşitlenecek ve x değerleri bulunacaktır. Örneğin, f'(x) = 2ax + b = 0 eşitliğinden, kritik noktaları x = -b / 2a olarak bulunur.

Konkavite

Fonksiyonun konkavitesi, maksimum veya minimum değerin bulunması için önemlidir. Konkavite, fonksiyonun eğiminin değişimini gösterir. Konkaviteyi bulmak için, ikinci dereceden türev alınır. Örneğin, f”(x) = 2a ikinci dereceden türevi, fonksiyonun konkaviteliğini gösterir.

Maksimum veya Minimum Değeri Bulma

Kritik noktaları ve konkaviteyi bulduktan sonra, maksimum veya minimum değeri bulunabilir. Eğer konkavite pozitif ise, kritik nokta maksimum değeri, eğer konkavite negatif ise, kritik nokta minimum değeri gösterir. Örneğin, f(x) = x^2 + 2x + 1 fonksiyonunun maksimum veya minimum değeri, x = -1 kritik noktasında bulunur.

Örnek Uygulama

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri bulma uygulamasına bir örnek olarak, bir şirketin kârı maksimize etmek için, maliyet fonksiyonunu minimize etmek gerekir. Örneğin, maliyet fonksiyonu, f(x) = x^2 + 2x + 1 şeklinde olabilir. Bu durumda, kritik noktaları x = -1 olarak bulunur ve konkaviteyi bulmak için, ikinci dereceden türev alınır. Konkavite pozitif ise, kritik nokta maksimum değeri, eğer konkavite negatif ise, kritik nokta minimum değeri gösterir.

Bir fonksiyonun maksimum ve minimum değerleri nasıl bulunur?

Bir fonksiyonun maksimum ve minimum değerlerini bulmak için ilk adım, fonksiyonun türevini bulmaktır. Türev, fonksiyonun eğiminin değişim oranını gösterir. Daha sonra, türevi sıfır yapan noktaları bulmak gerekir. Bu noktalar, fonksiyonun maksimum ve minimum değerlerini verecek noktalarıdır.

Fonksiyonun Türevi Nasıl Bulunur?

Fonksiyonun türevi, limit kavramı kullanılarak bulunur. Limit, bir noktadaki değerin, o noktaya yaklaştıkça değişim oranını gösterir. Türev formülü, (f(x+h) – f(x))/h şeklindedir. Burada, h, x’e yaklaşan bir değerdir. Türevi bulmak için, bu formülde h’yi sıfıra yaklaştırmak gerekir.

Maksimum ve Minimum Değerlerin Bulunma Şartları

Maksimum ve minimum değerlerin bulunma şartları, türevin sıfır olmasıdır. Yani, türevi sıfır yapan noktalar, fonksiyonun maksimum ve minimum değerlerini verir. Bu noktalar, kritik noktalar olarak adlandırılır. Kritik noktaların bulunma şartları, türevin sıfır olması ve ikinci türevin pozitif veya negatif olmasıdır.

İkinci Türev Yöntemi

İkinci türev yöntemi, maksimum ve minimum değerlerin bulunma yöntemlerinden biridir. Bu yöntemde, ikinci türevi bulmak gerekir. İkinci türev, fonksiyonun eğiminin değişim oranını gösterir. İkinci türevin pozitif olması durumunda, fonksiyonun minimum değeri, negatif olması durumunda, fonksiyonun maksimum değeri bulunur.

Konvex ve Konkav Fonksiyonlar

Konvex ve konkav fonksiyonlar, maksimum ve minimum değerlerin bulunma yöntemlerinde önemlidir. Konvex fonksiyonlar, maksimum değeri verirken, konkav fonksiyonlar, minimum değeri verir. Fonksiyonun konvex veya konkav olması, ikinci türevine göre belirlenir.

Fonksiyonun Grafik Çizimi

Fonksiyonun grafik çizimi, maksimum ve minimum değerlerin bulunma yöntemlerinde kullanılır. Grafik sayesinde, fonksiyonun maksimum ve minimum değerlerini görsel olarak belirlemek mümkün olur. Ayrıca, grafik, kritik noktaların bulunma şartlarını gösterir.

Parabolün minimum değeri nasıl bulunur?

Parabolün minimum değeri, parabolün en düşük noktasında bulunan değerdir. Bu değerin bulunması için birkaç yöntem vardır.

Parabolün Grafiği

Parabolün grafiği incelendiğinde, minimum değerin bulunduğu nokta, grafiğin en düşük noktasına karşılık gelir. Bu nokta, parabolün ekseni ile kesiştiği noktadır. Minimum değerin bulunması için, parabolün denklemi yazılarak, bunun türevi alınır. Daha sonra, türevin kökleri bulunur ve bu kökler, minimum değerin bulunduğu noktalara karşılık gelir.

Parabolün Denklemi

Parabolün denklemi, genel olarak ax^2 + bx + c şeklinde yazılır. Burada, a, b ve c katsayılarıdır. Minimum değerin bulunması için, bu denklem türevi alınarak, bunun kökleri bulunur. Örneğin, x^2 + 4x + 4 denklemi için, türevi 2x + 4 şeklindedir. Daha sonra, bu türevin kökleri bulunur ve minimum değerin bulunduğu nokta tespit edilir.

Türev Alma Yöntemi

Türev alma yöntemi, parabolün minimum değerin bulunması için en yaygın kullanılan yöntemidir. Bu yöntemde, parabolün denklemi türevi alınarak, bunun kökleri bulunur. Daha sonra, bu kökler, minimum değerin bulunduğu noktalara karşılık gelir. Örneğin, x^2 + 4x + 4 denklemi için, türevi 2x + 4 şeklindedir. Daha sonra, bu türevin kökleri bulunur ve minimum değerin bulunduğu nokta tespit edilir.

Minimum Değerin Özellikleri

Minimum değerin bulunması için, parabolün bazı özelliklerini bilmek gerekir. Örneğin, parabolün minimum değeri, sempre en düşük noktasında bulunur. Ayrıca, parabolün ekseni ile kesiştiği nokta, minimum değerin bulunduğu noktadır.

Uygulama Alanları

Parabolün minimum değerin bulunması, çeşitli alanlarda uygulanır. Örneğin, fizikte, bir cismin hareketi sırasında, minimum değerin bulunduğu nokta, cismin en düşük noktasına karşılık gelir. Ayrıca, ekonomide, bir şirketin maliyetinin minimum değerin bulunduğu nokta, şirketin en düşük maliyetine karşılık gelir. Bu nedenle, parabolün minimum değerin bulunması, birçok alanda önemli bir role sahiptir.

1. Minimum değerin bulunması için, parabolün denklemi yazılarak, bunun türevi alınır.
2. Türevin kökleri bulunur ve bu kökler, minimum değerin bulunduğu noktalara karşılık gelir.
3. Parabolün ekseni ile kesiştiği nokta, minimum değerin bulunduğu noktadır.
4. Minimum değerin bulunması, çeşitli alanlarda uygulanır.
5. Parabolün minimum değerin bulunması, birçok alanda önemli bir role sahiptir.

Absolute maximum and minimum nedir?

Absolute maksimum ve minimum, bir fonksiyonun verilen aralıkta aldığı en büyük ve en küçük değerlerdir. Bu değerler, fonksiyonun davranışı hakkında önemli bilgiler sağlar.

Mutlak Maksimum ve Minimum Nasıl Bulunur?

Mutlak maksimum ve minimum, ilk ve ikinci türev testleri ile bulunur. İlk türev testi, fonksiyonun kritik noktalarının bulunmasına yardımcı olur. Bu noktalar, fonksiyonun maksimum veya minimum değerlerine karşılık gelir. İkinci türev testi ise, kritik noktalarının maksimum veya minimum değerlerine karşılık geldiğini belirler.

Mutlak Maksimum ve Minimumün Önemi

Mutlak maksimum ve minimum, birçok alanda önemlidir. Örneğin, bir şirketin maksimum karını bulmak için mutlak maksimum değeri kullanılır. Ayrıca, bir mühendislik projesinde, minimum maliyeti bulmak için mutlak minimum değeri kullanılır.

Farklı Fonksiyonlarda Mutlak Maksimum ve Minimum

Farklı fonksiyonlarda mutlak maksimum ve minimum farklıdır. Örneğin, bir parabolik fonksiyonda, mutlak maksimum değeri, parabolün tepesinde bulunur. Bir sinusoidal fonksiyonda, mutlak maksimum değeri, fonksiyonun maksimum değerine karşılık gelir.

Mutlak Maksimum ve Minimumün Uygulamaları

Mutlak maksimum ve minimumün uygulamaları, günlük hayatta sıkça görülür. Örneğin, bir restoranın maksimum müşterisini bulmak için mutlak maksimum değeri kullanılır. Ayrıca, bir şehirdeki minimum suç oranını bulmak için mutlak minimum değeri kullanılır.

Mutlak Maksimum ve Minimumün Matematiksel Tanımı

Mutlak maksimum ve minimumün matematiksel tanımı, şu şekilde做yılır:

1. Fonksiyonun verilen aralıkta aldığı en büyük değeri, mutlak maksimum değeri olarak adlandırılır.
2. Fonksiyonun verilen aralıkta aldığı en küçük değeri, mutlak minimum değeri olarak adlandırılır.
3. İlk türev testi, kritik noktaların bulunmasına yardımcı olur.
4. İkinci türev testi, kritik noktalarının maksimum veya minimum değerlerine karşılık geldiğini belirler.
5. Mutlak maksimum ve minimum, fonksiyonun davranışı hakkında önemli bilgiler sağlar.

Mutlak maksimum, bir fonksiyonun verilen aralıkta aldığı en büyük değeri, mutlak minimum, bir fonksiyonun verilen aralıkta aldığı en küçük değeridür.

Minimum nokta nedir?

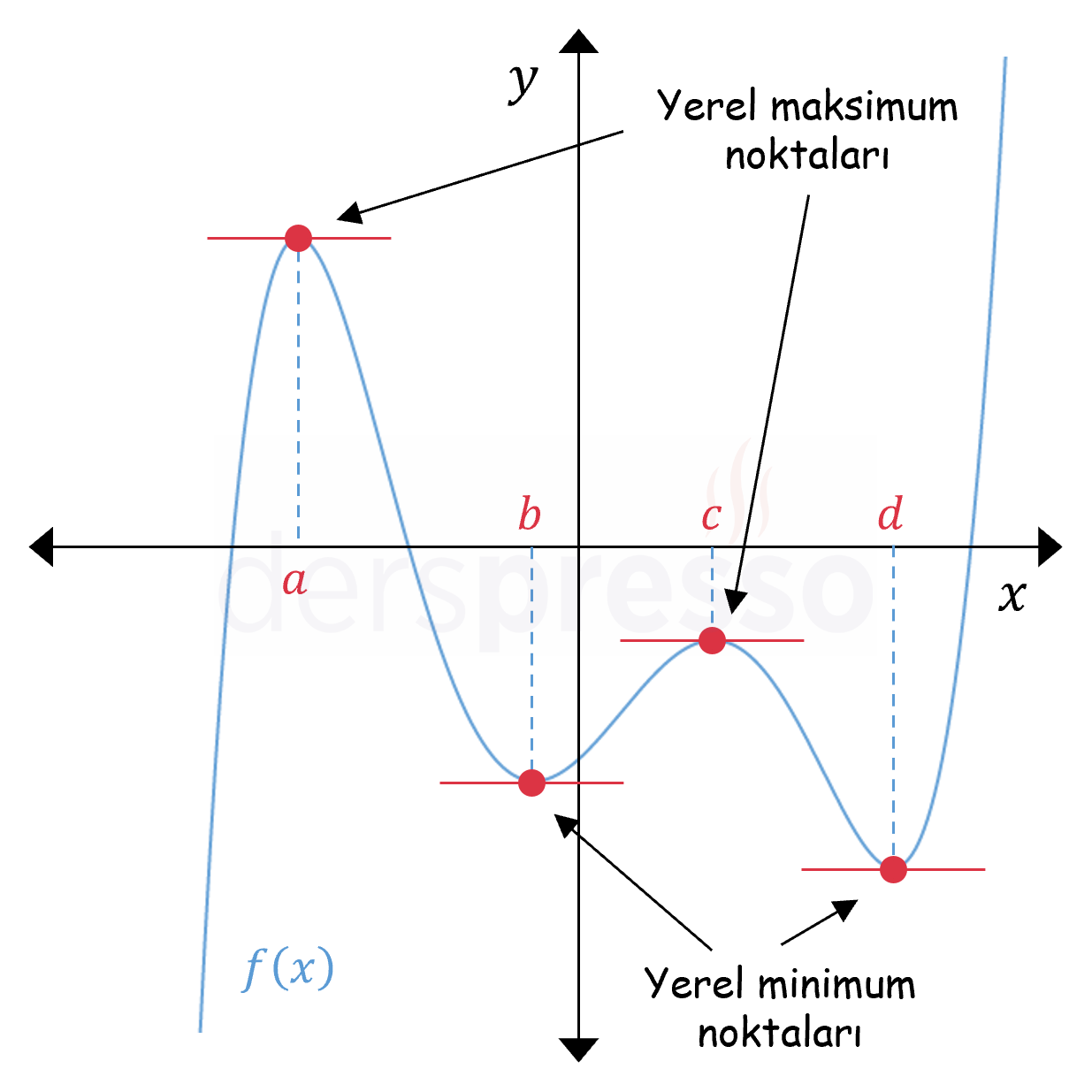
Minimum nokta, bir fonksiyonun veya bir ifadeenin en düşük değerini temsil eder. Bu nokta, fonksiyonun veya ifadenin azami değerinin altında kalan en düşük noktadır. Minimum nokta, matematiksel analizde, özellikle calculus ve optimize problemlerinde kullanılır.

Minimum Nokta Nasıl Bulunur?

Minimum nokta, bir fonksiyonun türevini alarak bulunabilir. Türev, fonksiyonun eğiminin bir noktasındaslopeını veren bir miktarıdır. Minimum nokta, türevin sıfır olduğu noktadır. Örneğin, f(x) = x^2 + 2x + 1 fonksiyonunun minimum noktasını bulmak için, önce türevini alırız: f'(x) = 2x + 2. Sonra, türevi sıfır olarak eşitleriz: 2x + 2 = 0. Çözümünü bulmak için, x’in değerini buluruz: x = -1. Sonuç olarak, fonksiyonun minimum noktası x = -1’dir.

Minimum Nokta Çeşitleri

Minimum nokta çeşitleri şunlardır:

1. Global minimum: Fonksiyonun tüm tanım alanındaki en düşük değeri.
2. Local minimum: Fonksiyonun belirli bir noktasındaki en düşük değeri.
3. Absolute minimum: Fonksiyonun tüm tanım alanındaki en düşük değeri, ancak bu değer fonksiyonun minimum noktasında olmayabilir.

Minimum Nokta Uygulamaları

Minimum nokta, birçok alanda uygulamaları vardır:

1. Optimizasyon: Minimum nokta, optimize problemlerinde kullanılır. Örneğin, bir şirketin maliyetini minimize etmek için, maliyet fonksiyonunun minimum noktasını bulmak gerekir.
2. Fizik: Minimum nokta, fiziksel sistemlerde kullanılır. Örneğin, bir cismin potansiyel enerji fonksiyonunun minimum noktasını bulmak, cismin dengedeki konumunu belirlemek için kullanılır.
3. Mühendislik: Minimum nokta, mühendislik problemlerinde kullanılır. Örneğin, bir köprünün maliyetini minimize etmek için, köprünün uzunluğunun minimum noktasını bulmak gerekir.

Minimum Nokta Avantajları

Minimum nokta, birçok avantaja sahiptir:

1. Maliyet minimizasyonu: Minimum nokta, maliyetlerin minimize edilmesine yardımcı olur.
2. Verimli kullanım: Minimum nokta, kaynakların verimli kullanımını sağlar.
3. Dengedeki konum: Minimum nokta, sistemlerin dengedeki konumunu belirlemek için kullanılır.

Minimum Nokta Sınırlamaları

Minimum nokta, bazı sınırlamalara sahiptir:

1. Fonksiyonun tanım alanı: Minimum nokta, fonksiyonun tanım alanı dışındayken bulunamaz.
2. Fonksiyonun sürekli olması: Minimum nokta, fonksiyonun sürekli olması gerekir.
3. Fonksiyonun türevi: Minimum nokta, fonksiyonun türevinin bulunmasına bağlıdır.

Daha fazla bilgi

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri nasıl bulunur?

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri, fonksiyonun grafik analizine dayanarak bulunur. Grafik analizinde, fonksiyonun maksimum veya minimum noktasını bulmak için, ilk olarak fonksiyonun türevini alırız. Türev, fonksiyonun eğiminin değeri olup, maksimum veya minimum noktasında eğimin sıfır olduğu bilinir. Böylece, türevi sıfır yapan noktanın koordinatlarını buluruz. Daha sonra, bu koordinatları fonksiyona yerine koyarak, maksimum veya minimum değeri hesaplarız.

Fonksiyonun maksimum veya minimum değeri hangi durumlarda bulunur?

Fonksiyonun maksimum veya minimum değeri, fonksiyonun sınır değerlerine ulaştığı durumlarda bulunur. Sınır değerleri, fonksiyonun tanım alanında bulunan en küçük veya en büyük değerlerdir. Ayrıca, fonksiyonun çiftlik noktasında da maksimum veya minimum değeri bulunur. Çiftlik noktası, fonksiyonun tanım alanında bulunan ve fonksiyonun değeri değişmeyen noktadır.

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri nasıl yorumlanır?

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri, fonksiyonun maksimum veya minimum noktasındaki değeridir. Bu değer, fonksiyonun tanım alanında bulunan en küçük veya en büyük değeridir. Maksimum veya minimum değeri, fonksiyonun en yüksek veya en düşük noktasını gösterir. Örneğin, bir şirketin kâr fonksiyonunda, maksimum değeri, şirketin en yüksek kâr elde ettiği noktadır.

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri hangi alanlarda kullanılır?

İkinci dereceden bir fonksiyonun maksimum veya minimum değeri, ekonomi, mühendislik, fizik ve istatistik gibi alanlarda kullanılır. Örneğin, ekonomide, bir şirketin kâr fonksiyonunda maksimum değeri, şirketin en yüksek kâr elde ettiği noktadır. Mühendislikte, bir köprünün inşaasında, maksimum değeri, köprünün en yüksek noktasında bulunur. Fizikte, bir cismin hareketi sırasında, maksimum değeri, cismin en yüksek hızına ulaştığı noktadır.