İçler Dışlar Çarpımı Nasıl Yapılır?

İçler dışlar çarpımı, özellikle mühendislik, fizik ve matematik alanlarında sıklıkla kullanılan bir kavramdır. İki vektörün çarpımından elde edilen sonuç, bu vektörlerin yönelimleri ve büyüklükleri arasındaki ilişkiyi gösterir. Ancak, bu çarpımın nasıl yapıldığını bilmek, özellikle yeni başlayanlar için zor olabilir. Bu yüzden, bu yazıda, içler dışlar çarpımının nasıl yapıldığını adım adım açıklayacağız. Çarpımın matematiksel tanımından, uygulamalarına kadar, tüm detayları ele alacağız.

İç Çarpım Dış Çarpım Nasıl Yapılır?

İç çarpım ve dış çarpım, matematikteki iki önemli kavramdır. Bunlar, vektörlerin çarpımı ile ilgili iki farklı yöntemidir.

İç çarpım, iki vektörün arasındaki açıyı ölçmeye yardımcı olur. İç çarpım, skalar bir değerdir ve iki vektörün arasındaki açı ile ilgili bilgi sağlar.

İç çarpım, aşağıdaki formülle hesaplanır:

A · B = |A| |B| cos(θ)

Burada, A ve B vektörler, |A| ve |B| bunların uzunlukları, θ ise iki vektör arasındaki açıyı gösterir.

İç Çarpımın Özellikleri

İç çarpımın bazı önemli özellikleri şunlardır:

1. İç çarpım, skalar bir değerdir.
2. İç çarpım, iki vektörün arasındaki açı ile ilgili bilgi sağlar.
3. İç çarpım, komütatif bir işlemidir, yani A · B = B · A.
4. İç çarpım, distribütif bir işlemidir, yani A · (B + C) = A · B + A · C.
5. İç çarpım, sıfır vektör ile çarpımında sonucu sıfır olur.

Dış Çarpımın Tanımı

Dış çarpım, iki vektörün arasındaki dış ürün üreten bir işlemidir. Dış çarpım, vektörel bir değerdir ve iki vektörün arasındaki açı ile ilgili bilgi sağlamaz.

Dış çarpım, aşağıdaki formülle hesaplanır:

A × B = (Ay Bz – Az By, Az Bx – Ax Bz, Ax By – Ay Bx)

Burada, A ve B vektörler, Ax, Ay, Az ve Bx, By, Bz bunların bileşenleridir.

Dış Çarpımın Özellikleri

Dış çarpımın bazı önemli özellikleri şunlardır:

1. Dış çarpım, vektörel bir değerdir.
2. Dış çarpım, iki vektörün arasındaki açı ile ilgili bilgi sağlamaz.
3. Dış çarpım, antisimetrik bir işlemidir, yani A × B = – B × A.
4. Dış çarpım, distribütif bir işlemidir, yani A × (B + C) = A × B + A × C.
5. Dış çarpım, sıfır vektör ile çarpımında sonucu sıfır olur.

İç Çarpımın Uygulamaları

İç çarpım, birçok alanda kullanılır. Bazı önemli uygulamaları şunlardır:

1. Fizik{: Fizikteki birçok problemde, iç çarpım kullanılır. Örneğin, kuvvet ve yer değiştirme arasındaki ilişkiyi bulmak için iç çarpım kullanılır.}
2. Mühendislik{: Mühendislikteki birçok problemde, iç çarpım kullanılır. Örneğin, yapısal analizlerde, iç çarpım kullanılır.}
3. Bilgisayar Grafikleri{: Bilgisayar grafiklerindeki birçok problemde, iç çarpım kullanılır. Örneğin, 3D modelleme ve aydınlatmada, iç çarpım kullanılır.}

Dış Çarpımın Uygulamaları

Dış çarpım, birçok alanda kullanılır. Bazı önemli uygulamaları şunlardır:

1. Fizik{: Fizikteki birçok problemde, dış çarpım kullanılır. Örneğin, manyetik alan ve elektrik alan arasındaki ilişkiyi bulmak için dış çarpım kullanılır.}
2. Mühendislik{: Mühendislikteki birçok problemde, dış çarpım kullanılır. Örneğin, elektrik mühendisliğinde, dış çarpım kullanılır.}
3. Bilgisayar Grafikleri{: Bilgisayar grafiklerindeki birçok problemde, dış çarpım kullanılır. Örneğin, 3D modelleme ve aydınlatmada, dış çarpım kullanılır.}

Içler dışlar nasıl çarpılır?

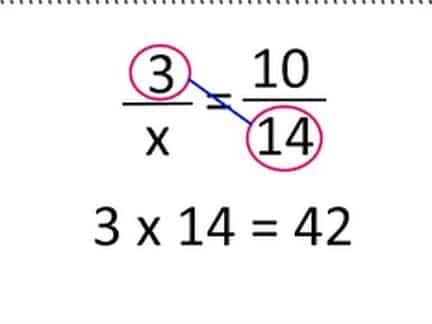
İçler dışlar çarpıma işlemini anlamak için önce içler dışları tanımamız gerekir. İçler dışlar, bir sayının kendi içindeki rakamların çarpım sonucu elde edilen sayıdır. Örneğin, 456 sayısının içler dışları, 456 = 120’dir.

İçler Dışlar Çarpımının Özellikleri

İçler dışlar çarpımının önemli özellikleri şunlardır:

1. İçler dışlar çarpımında sıfırın etkisi: Sıfır içeren bir sayının içler dışları, her zaman sıfır olacaktır.
2. İçler dışlar çarpımında tek ve çift sayıların etkisi: Tek sayıların içler dışları, tek bir sayıdır. Çift sayıların içler dışları, çift bir sayıdır.
3. İçler dışlar çarpımının simetri özelliği: İçler dışlar çarpımında, rakamların yer değiştirmesi, sonuçta bir değişiklik yapmaz.

İçler Dışlar Çarpımında Sayıların Gruplanması

İçler dışlar çarpımında sayılar, gruplanarak çarpım işlemi yapılabilir. Örneğin, 456 sayısının içler dışları, (45)6 = 120’dir.

İçler Dışlar Çarpımında Rakamların Tekrarı

İçler dışlar çarpımında, bir rakamın tekrarı, sonuçta bir değişiklik yapmaz. Örneğin, 444 sayısının içler dışları, 444 = 64’tür.

İçler Dışlar Çarpımında Rakamların Sırası

İçler dışlar çarpımında, rakamların sırası, sonuçta bir değişiklik yapmaz. Örneğin, 123 sayısının içler dışları, 123 = 6’dır.

İçler Dışlar Çarpımının Uygulama Alanları

İçler dışlar çarpımının uygulama alanları şunlardır:

1. Matematik problemlerinde: İçler dışlar çarpımına, matematik problemlerinde çözümlemenin bir adımında kullanılır.
2. Kriptolojide: İçler dışlar çarpımına, kriptolojide şifreleme ve deşifreleme işlemlerinde kullanılır.
3. Bilgisayar bilimlerinde: İçler dışlar çarpımına, bilgisayar bilimlerinde algoritmaların geliştirilmesinde kullanılır.

İçler dışlar çarpımı kaçıncı sınıf konusu?

İçler dışlar çarpımı, matematiğin temel konularından biri olup, çarpım ve bölüm işlemlerinde kullanılan bir yöntemdir. Bu yöntem, içler ve dışlar olarak adlandırılan iki türlü çarpım şeklinden oluşur.

İçler Dışlar Çarpımının Tanımı

İçler dışlar çarpımı, iki sayısal ifadelerin çarpımında kullanılan bir yöntemdir. Bu yöntemde, içler olarak adlandırılan sayısal ifadeler, çarpım işleminde dışlar olarak adlandırılan sayısal ifadelerle çarpılır.

İçler Dışlar Çarpımının Önemi

İçler dışlar çarpımı, matematik ve fen bilimlerinde kullanılan bir yöntemdir. Bu yöntem, problemlerin çözümünde ve formüllerin oluşturulmasında kullanılan bir araçtır.

İçler Dışlar Çarpımının Sınıflandırılması

İçler dışlar çarpımı, ilköğretim ve ortaöğretim sınıflarında öğrenilir. Bu yöntem, 6. sınıf ve 7. sınıf konuları arasında yer alır.

İçler Dışlar Çarpımının Uygulama Alanları

İçler dışlar çarpımı, fizik, kimya, biyoloji ve mühendislik gibi alanlarda kullanılır. Bu yöntem, problemlerin çözümünde ve formüllerin oluşturulmasında kullanılan bir araçtır.

İçler Dışlar Çarpımının Avantajları

İçler dışlar çarpımının avantajları şunlardır:

1. Zaman kazandırır: İçler dışlar çarpımı, problemlerin çözümünde kullanılan bir yöntemdir.
2. Basitlik sağlar: Bu yöntem, karmaşık problemlerin çözümünde kullanılan bir araçtır.
3. Geniş uygulama alanı: İçler dışlar çarpımı, çeşitli alanlarda kullanılan bir yöntemdir.

Eşitlikte içler dışlar çarpımı yapılır mı?

Eşitlikte içler dışlar çarpımı yapılır. Bu işlem, matematiksel eşitlikler arasında gerçekleştirilir. Eşitliğin her iki tarafında bulunan içler dışlar çarpımı sonucu eşitlikte değişiklik olmaz.

Eşitlikte İçler Dışlar Çarpımının Önemi

Eşitlikte içler dışlar çarpımının önemi, matematiksel işlemlerin basitleştirilmesi ve eşitliklerin çözümlenmesi sonucu bulunur. İçler dışlar çarpımı, eşitliğin her iki tarafında bulunan ifadelerin basitleştirilmesine yardımcı olur.

Eşitlikte İçler Dışlar Çarpımının Uygulama Alanları

Eşitlikte içler dışlar çarpımının uygulama alanları çeşitlidir:

1. Cebir: Eşitlikte içler dışlar çarpımı, cebirde eşitliklerin çözümlenmesi sonucu kullanılır.
2. Geometri: Eşitlikte içler dışlar çarpımı, geometride eşitliklerin çözümlenmesi sonucu kullanılır.
3. Trigonometri: Eşitlikte içler dışlar çarpımı, trigonometride eşitliklerin çözümlenmesi sonucu kullanılır.

Eşitlikte İçler Dışlar Çarpımının Avantajları

Eşitlikte içler dışlar çarpımının avantajları şunlardır:

1. Basitleştirme: Eşitlikte içler dışlar çarpımı, eşitliğin her iki tarafında bulunan ifadelerin basitleştirilmesine yardımcı olur.
2. Çözümleme: Eşitlikte içler dışlar çarpımı, eşitliklerin çözümlenmesi sonucu kullanılır.
3. Zaman Tasarrufu: Eşitlikte içler dışlar çarpımı, eşitliklerin çözümlenmesi sonucu zaman tasarrufu sağlar.

Eşitlikte İçler Dışlar Çarpımının Uygulama Örnekleri

Eşitlikte içler dışlar çarpımının uygulama örnekleri şunlardır:

1. 2x + 3 = 5 eşitliğinde, her iki tarafında bulunan içler dışlar çarpımı sonucu eşitlikte değişiklik olmaz.
2. x^2 + 4x – 5 = 0 eşitliğinde, her iki tarafında bulunan içler dışlar çarpımı sonucu eşitlikte değişiklik olmaz.
3. sin(x) + cos(x) = 1 eşitliğinde, her iki tarafında bulunan içler dışlar çarpımı sonucu eşitlikte değişiklik olmaz.

Eşitlikte İçler Dışlar Çarpımının Hataları

Eşitlikte içler dışlar çarpımının hataları şunlardır:

1. Eşitliğin bozulması: Eşitlikte içler dışlar çarpımı sonucu eşitliğin bozulması durumunda, eşitliğin çözümlenmesi sonucu yanlış sonuçlar elde edilir.
2. İfade hataları: Eşitlikte içler dışlar çarpımı sonucu ifade hataları durumunda, eşitliğin çözümlenmesi sonucu yanlış sonuçlar elde edilir.
3. Kesin olmayan sonuçlar: Eşitlikte içler dışlar çarpımı sonucu kesin olmayan sonuçlar durumunda, eşitliğin çözümlenmesi sonucu yanlış sonuçlar elde edilir.

Çapraz Çarpım nasıl yapılır?

Çapraz çarpım, iki vektörün çarpımı sonucu üçüncü bir vektör elde edilmesidir. Bu çarpım, üç boyutlu uzayda iki vektörün doğrultularının çarpımı sonucu elde edilir. Çapraz çarpım, skaler çarpım ile karıştırılmamalıdır, çünkü skaler çarpım sonucu bir sayı elde edilir, ancak çapraz çarpım sonucu bir vektör elde edilir.

Çapraz Çarpımın Tanımı

Çapraz çarpım, iki vektörün çarpımı sonucu üçüncü bir vektör elde edilmesidir. Bu çarpım, üç boyutlu uzayda iki vektörün doğrultularının çarpımı sonucu elde edilir. Çapraz çarpım, vektörel çarpım olarak da bilinir.

Çapraz Çarpımın Formülü

Çapraz çarpımın formülü şu şekilde verilir:

a × b = (a₂b₃ – a₃b₂, a₃b₁ – a₁b₃, a₁b₂ – a₂b₁)

Burada, a ve b, çapraz çarpım sonucu elde edilen vektörlerdir.

Çapraz Çarpımın Özellikleri

Çapraz çarpımın bazı özellikleri şunlardır:

1. Çapraz çarpım, antisimetrik bir çarpımdır, yani a × b = -(b × a)
2. Çapraz çarpım, distribütif bir çarpımdır, yani a × (b + c) = a × b + a × c
3. Çapraz çarpım, sıfır vektörünü içerir, yani a × 0 = 0

Çapraz Çarpımın Uygulamaları

Çapraz çarpım, çeşitli alanlarda uygulanır, bunlar:

1. Fizik: Çapraz çarpım, kuvvet ve moment hesaplamalarında kullanılır.
2. Mühendislik: Çapraz çarpım, yapısal analizlerde ve mekanik hesaplamalarında kullanılır.
3. Bilgisayar Grafikleri: Çapraz çarpım, 3D grafik hesaplamalarında kullanılır.

Çapraz Çarpımın Avantajları

Çapraz çarpımın bazı avantajları şunlardır:

1. Çapraz çarpım, üç boyutlu uzayda iki vektörün çarpımını sağlar.
2. Çapraz çarpım, vektörel çarpım sonucu elde edilen vektörünü verir.
3. Çapraz çarpım, hesaplamaları basitleştirir.

Daha fazla bilgi

İçler Dışlar Çarpımı Nedir?

İçler dışlar çarpımı, vektörlerin çarpımı olarak bilinen bir matematiksel operasyondur. Bu operasyon, iki vektörün eleman eleman çarpımını hesaplamak için kullanılır. Örneğin, A = (a1, a2, a3) ve B = (b1, b2, b3) olmak üzere iki vektörümüz varsa, içler dışlar çarpımı aşağıdaki biçimde hesaplanır: A × B = (a1b1, a2b2, a3b3). Bu operasyon, fizik, mühendislik ve bilgisayar bilimlerinde yaygın olarak kullanılır.

İçler Dışlar Çarpımı Nasıl Yapılır?

İçler dışlar çarpımı, vektörlerin coordinatlarına göre yapılır. Önce, iki vektörün coordinatlarını belirleyerek başlamalıyız. Örneğin, A = (a1, a2, a3) ve B = (b1, b2, b3) olmak üzere iki vektörümüz varsa, coordinatlarını belirledikten sonra, çarpım işlemini gerçekleştiriyoruz. Çarpım işlemini gerçekleştirmek için, her bir coordinatı çarpımını hesaplıyoruz. Örneğin, A × B = (a1b1, a2b2, a3b3). Sonuç olarak, içler dışlar çarpımı, vektörlerin coordinatlarına göre hesaplanan bir çarpım operasyonudur.

İçler Dışlar Çarpımı Ne İçin Kullanılır?

İçler dışlar çarpımı, fizik, mühendislik ve bilgisayar bilimlerinde yaygın olarak kullanılır. Örneğin, mekanikte, içler dışlar çarpımı, moment hesaplamak için kullanılır. Ayrıca, elektrik mühendisliğinde, içler dışlar çarpımı, elektrik alanları hesaplamak için kullanılır. Bunun dışında, bilgisayar bilimlerinde, içler dışlar çarpımı, grafik hesaplamalarda kullanılır. Kısaca, içler dışlar çarpımı, çeşitli alanlarda, vektörlerin çarpımı hesaplamak için kullanılır.

İçler Dışlar Çarpımı ile Diğer Çarpım Operasyonları Arasında Ne Fark Var?

İçler dışlar çarpımı, diğer çarpım operasyonlarından farklıdır. Örneğin, skaler çarpım, vektörlerin uzunluklarını hesaplamak için kullanılır, ancak içler dışlar çarpımı, vektörlerin coordinatlarına göre hesaplanan bir çarpım operasyonudur. Ayrıca, dış çarpım, vektörlerin dış çarpımını hesaplamak için kullanılır, ancak içler dışlar çarpımı, vektörlerin eleman eleman çarpımını hesaplamak için kullanılır. Kısaca, içler dışlar çarpımı, diğer çarpım operasyonlarından farklıdır ve kendine özgü özellikleri vardır.