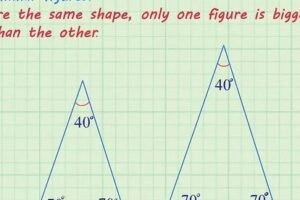
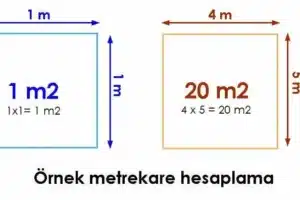
Bir Üçgenin Alanı Nasıl Hesaplanır?
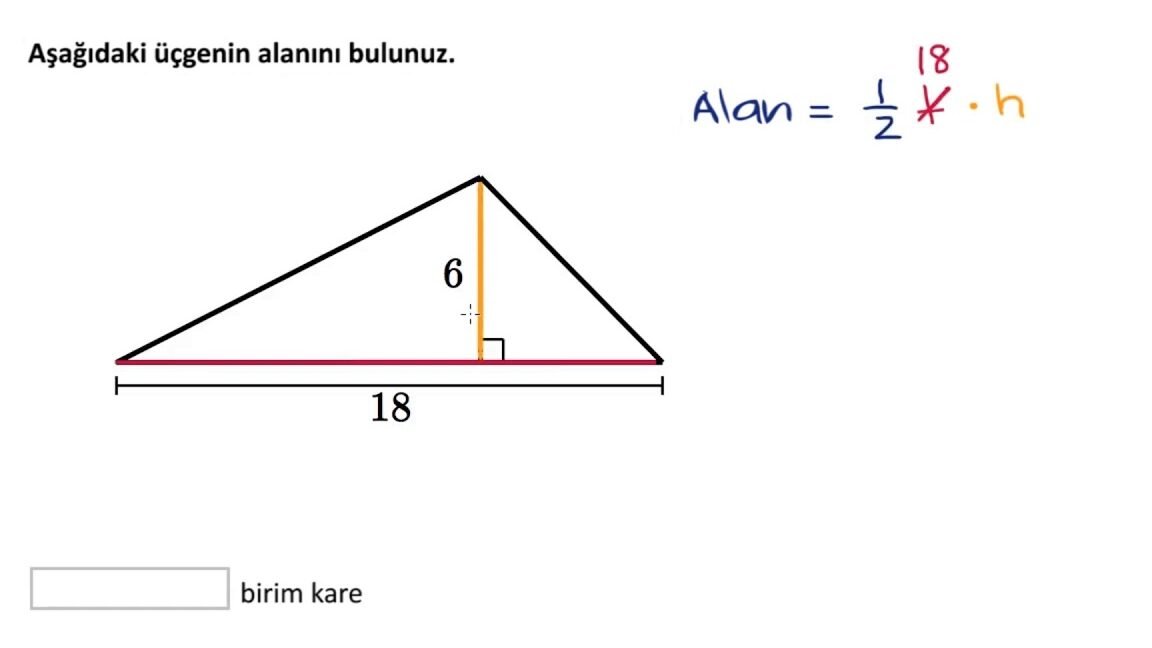
Üçgenin alanı, geometrinin temel kavramlarından biridir ve günlük hayatımızda sıkça karşımıza çıkar. özellikle mimarlık, mühendislik ve tasarım alanlarında üçgenin alanı hesaplanarak, alanların boyutları ve şekilleri belirlenir. Ancak, üçgenin alanı nasıl hesaplandığını bilmeyenler için bu kavram karmaşık ve uzak görünür. Bu yazıda, üçgenin alanını hesaplamak için kullanılan temel yöntemleri ve formülleri ele alacağız.
Bir Üçgenin Alanı Nasıl Hesaplanır?
Üçgenin alanı, temel olarak üç kenar uzunluğunun bilinmesi durumunda hesaplanabilir. Ancak, kenar uzunluklarının bilinmediği durumlarda, değişik formüller ve yöntemler kullanılır.
Üçgenin Alanı Formülü
Üçgenin alanı, aşağıdaki formülle hesaplanır:
Domatesler Nasıl Budanır?Alan = (a b) / 2
Burada, a ve b, üçgenin iki kenar uzunluğudur. Bu formül, özellikle dik üçgenlerde kullanılır.
Kenar Uzunluklarının Bilinmediği Durumlarda
Kenar uzunluklarının bilinmediği durumlarda, aşağıdaki yöntemler kullanılır:
Erkek Arkadaşının Telefonunda Bir Şey Saklayıp Saklamadığını Anlamak?Heron Formülü: Bu formül, üçgenin üç kenar uzunluğunu kullanarak alanı hesaplar. Formül şu şekildedir:
Alan = √(s(s-a)(s-b)(s-c))
Burada, s, üçgenin yarı çevre uzunluğudur. a, b ve c, üçgenin kenar uzunluklarıdır.
Benzerlik Oranı Nasıl Bulunur?Koordinatlar ile Hesaplama: Bu yöntemde, üçgenin köşelerinin koordinatları kullanılır. Üçgenin alanı, aşağıdaki formülle hesaplanır:
Alan = |(x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)) / 2|
Burada, (x1, y1), (x2, y2) ve (x3, y3), üçgenin köşelerinin koordinatlarıdır.
Bir Kızın Belki Demesine Cevap Vermenin 10 Kolay Yolu| Üçgenin Alanı Formülü | Kullanım Alanı |
|---|---|
| (a b) / 2 | Dik Üçgenler |
| √(s(s-a)(s-b)(s-c)) | Üçgenin Üç Kenar Uzunluğunu Kullanarak |
| |(x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)) / 2| | Koordinatlar ile Hesaplama |
Üçgenin Çeşitleri ve Alanı
Üçgenin çeşitleri, alan hesaplamasında önemli bir role sahiptir. Örneğin, dik üçgenlerde, yukarıdaki formül kullanılır. Eşkenar üçgenlerde, kenar uzunlukları eşit olduğu için, alan hesaplaması daha kolaydır.
Alan Hesaplamasında Dikkat Edilmesi Gerekenler
Alan hesaplamasında, dikkat edilmesi gerekenler şunlardır:
Üçgenin köşelerinin doğru bir şekilde belirlenmesi
Kenar uzunluklarının doğru bir şekilde ölçülmesi
Formüllerin doğru bir şekilde uygulanması
Üçgenin Alanı Hesaplamasının Uygulama Alanları
Üçgenin alanı hesaplamasının uygulama alanları şunlardır:
Mühendislik: İnşaat mühendisliği, makine mühendisliği gibi alanlarda kullanılır.
Coğrafya: Coğrafya biliminde, üçgenin alanı hesaplamaları kullanılır.
Matematik: Matematik biliminde, üçgenin alanı hesaplamaları kullanılır.
Bir üçgenin alanı nasıl bulunur?
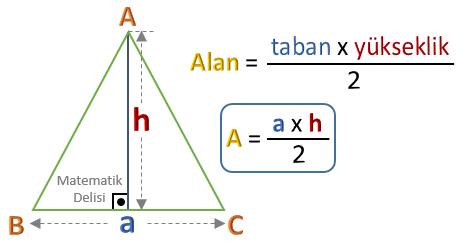
Üçgenin alanı, uzunluğu ve genişliği bilinen bir dik üçgende, Alan Formülü kullanılarak bulunur. Bu formül, uzunluğu a ve genişliği b olan bir dik üçgende, alanı hesaplamak için kullanılır: Alan = (a b) / 2.
Üçgenin Çeşitleri
Üçgenler çeşitlerine göre alan hesaplamaları farklılık gösterir. Örneğin:
- Dik üçgende, uzunluğu ve genişliği bilinen bir dik üçgende, alanı hesaplamak için Alan Formülü kullanılır.
- Eşkenar üçgende, kenar uzunluğu bilinen bir eşkenar üçgende, alanı hesaplamak için Alan = (kenar kenar √3) / 4 formülü kullanılır.
- Çokgen üçgende, kenar uzunluğu ve açıları bilinen bir çokgen üçgende, alanı hesaplamak için Alan = (kenar kenar sin(açı)) / 2 formülü kullanılır.
Üçgenin Özellikleri
Üçgenin özellikleri, alanı hesaplamak için kullanılır. Örneğin:
- Üçgenin uzunluğu ve genişliği, alanı hesaplamak için kullanılır.
- Üçgenin açıları, alanı hesaplamak için kullanılır.
- Üçgenin kenarları, alanı hesaplamak için kullanılır.
Üçgenin Alan Hesaplamaları
Üçgenin alan hesaplamaları, çeşitlerine göre farklılık gösterir. Örneğin:
- Dik üçgende, uzunluğu ve genişliği bilinen bir dik üçgende, alanı hesaplamak için Alan Formülü kullanılır.
- Eşkenar üçgende, kenar uzunluğu bilinen bir eşkenar üçgende, alanı hesaplamak için Alan = (kenar kenar √3) / 4 formülü kullanılır.
Üçgenin Uygulamaları
Üçgenin uygulamaları, çeşitlerine göre farklılık gösterir. Örneğin:
- Mimarlıkta, üçgenler, binaların tasarımında kullanılır.
- Fizikte, üçgenler, kuvvetlerin ve momentlerin hesaplanmasında kullanılır.
- Matematikte, üçgenler, geometrik hesaplamalarda kullanılır.
Üçgenin Tarihçesi
Üçgenin tarihçesi, antik çağlara kadar uzanır. Örneğin:
- Antik Yunanda, üçgenler, geometrik hesaplamalarda kullanılır.
- İlk Çağda, üçgenler, mimarlıkta kullanılır.
- Modern Çağda, üçgenler, fizikte ve matematikte kullanılır.
3 kenarı bilinen üçgenin alanı nasıl hesaplanır?
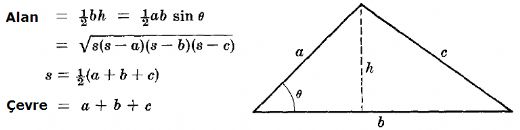
Bir üçgenin alanını hesaplamak için, üç kenar uzunluğunu biliyor olmanız gerekir. Bu durumda, Heron’un Formülü kullanılır. Heron’un Formülü, bir üçgenin alanını hesaplamak için kullanılan bir matematiksel formüldür.
Üçgenin Alanını Hesaplamak için Gerekli Bilgiler
Üçgenin alanını hesaplamak için, aşağıdaki bilgileri bilmemiz gerekir:
- Üç kenar uzunluğu (a, b, c)
- Üçgende herhangi bir açı bilgisine gerek yoktur
- Heron’un Formülü kullanılarak alan hesaplanır
Heron’un Formülü Nedir?
Heron’un Formülü, bir üçgenin alanını hesaplamak için kullanılan bir matematiksel formüldür. Formül, M.Ö. 100 yılında Heron tarafından keşfedilmiştir. Formül şöyledir:
s = (a + b + c) / 2
Alan = √(s(s-a)(s-b)(s-c))
Üçgenin Alanını Hesaplamak için Adımlar
Üçgenin alanını hesaplamak için aşağıdaki adımları takip ediniz:
- Üç kenar uzunluğunu (a, b, c) bulunuz
- s değeri için formülünü uygulayınız: s = (a + b + c) / 2
- Alan değeri için formülünü uygulayınız: Alan = √(s(s-a)(s-b)(s-c))
- Alan değeri sonucunu alın
Üçgenin Alanını Hesaplamak için Örnek
Örnek olarak, bir üçgenin kenar uzunlukları 5, 6 ve 7 ise, alanını hesaplamak için aşağıdaki adımları takip ediniz:
- a = 5, b = 6, c = 7
- s = (5 + 6 + 7) / 2 = 9
- Alan = √(9(9-5)(9-6)(9-7)) = 14.7
Üçgenin Alanını Hesaplamak için Uygulamaları
Üçgenin alanını hesaplamak için çeşitli uygulamaları vardır:
- Mimarlık ve inşaat mühendisliğinde alan hesaplamak için kullanılır
- Coğrafya ve haritacılık alanında alan hesaplamak için kullanılır
- Fizik ve mühendislik alanında alan hesaplamak için kullanılır
3 4 5 üçgeninin alanı nedir?
3, 4, 5 üçgeninin alanı nedir?
Üçgenin alanı, Pitagor teoremi‘ne göre, a² + b² = c² формуласına göre hesaplanır. Burada a = 3, b = 4, c = 5 olarak verilmiştir. Üçgenin alanı, yarı çevre uzunluğunun kareköküdür. Yani, alanı = √(s(s-a)(s-b)(s-c)) formülüne göre hesaplanır. Burada s = (a + b + c) / 2 olarak bulunur.
Üçgenin Alanını Bulma Yöntemleri
Üçgenin alanı, verschillende yöntemlerle bulunur. Bunlar:
- Pitagor teoremi: a² + b² = c² formülünü kullanarak üçgenin alanını bulmak mümkündür.
- Yarı çevre uzunluğu: yarı çevre uzunluğunun karekökü alınarak üçgenin alanı bulunur.
- Kenar uzunlukları: üçgenin kenar uzunlukları kullanılarak alanı bulunur.
Üçgenin Çeşitleri
Üçgenler, çeşitlerine göre sınıflandırılır. Bunlar:
- İkizkenar üçgen: iki kenarı eşit olan üçgendir.
- Çokgen üçgen: üç veya daha fazla kenarı olan üçgendir.
- Dik üçgen: bir açısı 90 derece olan üçgendir.
Pitagor Teoremi
Pitagor teoremi, dik üçgende kullanılan bir formüldür. Bu formül, a² + b² = c² olarak verilir. Burada a ve b, dik üçgende bulunan iki kenardır, c ise hipotenüsdür.
Üçgenin Özellikleri
Üçgenin bazı özellikleri şunlardır:
- Kenar uzunlukları: üçgenin kenar uzunlukları kullanılır.
- Açılar: üçgenin açıları kullanılır.
- Alan: üçgenin alanı bulunur.
Üçgenin Uygulamaları
Üçgenin uygulamaları şunlardır:
- Mimarlık: üçgenler, mimaride kullanılan önemli şekillerdir.
- İnşaat: üçgenler, inşaatlarda kullanılan şekillerdir.
- Matematik: üçgenler, matematikte kullanılan şekillerdir.
Yüksekliği olmayan üçgenin alanı nasıl bulunur?

Üçgenin alanı, yüksekliği bilinmeyen durumlarda, çeşitli yöntemler kullanılarak bulunabilir. Bunlar arasında en yaygın olanlar, kenar uzunlukları bilinen üçgen için Heron’un Formülü ve kenar uzunlukları ve bir açı bilinen üçgen için çarpım formülü kullanılır.
Kenar Uzunlukları Bilinmeyen Üçgen için Alan Bulma
Bu durumda, Heron’un Formülü kullanılır. Formül, üçgenin yarı çevre uzunluğunun karesinden, kenar uzunluklarının karelerinin toplamını çıkartarak bulunur. Formül şöyledir:
- Üçgenin yarı çevre uzunluğu (s) bulunur: s = (a + b + c) / 2
- Alan (A) bulunur: A = √(s(s-a)(s-b)(s-c))
Kenar Uzunlukları ve Bir Açı Bilinen Üçgen için Alan Bulma
Bu durumda, çarpım formülü kullanılır. Formül, bir kenar uzunluğu ve karşıt açıyı kullanarak bulunur. Formül şöyledir:
- Alan (A) bulunur: A = (b c sin(A)) / 2
Üçgenin Sınıfı ve Alan Bulma
Üçgenlerin sınıflandırılması, alan bulma yöntemini değiştirebilir. Örneğin, eşkenar üçgen için, alan, kenar uzunluğunun karesinin yarısı olarak bulunur. İkizkenar üçgen için, alan, taban uzunluğu ve yüksekliğinin çarpımına eşitlenir.
Alan Bulma için Kullanılan Araçlar
Alan bulma işlemi için, çeşitli araçlar kullanılır. Bunlar arasında, hesap makineleri, bilgisayar programları ve çizim araçları sayılabilir.
Üçgenin Alanı ve Uygulamaları
Üçgenin alanı, çeşitli uygulama alanlarında kullanılır. Örneğin, mimarlık, inşaat, coeğrafya ve fizik gibi alanlarda, üçgenin alanı, problemlerin çözümü için kullanılır.
Daha fazla bilgi
Üçgenin Alanı Nasıl Hesaplanır?
Üçgenin alanı, kenar uzunlukları ve açılar kullanılarak hesaplanabilir. Üçgenin alanı, genellikle Heron’s Formula ile hesaplanır. Bu formül, üçgenin kenar uzunluklarını kullanarak alanını hesaplar. Formül, a, b ve c kenar uzunluklarını kullanarak şu şekilde hesaplanır: Alan = √(s(s-a)(s-b)(s-c)) burada s, üçgenin yarı çevre uzunluğudur.
Üçgenin Taban ve Yüksekliği Nasıl Bulunur?
Üçgenin taban ve yüksekliği, üçgendeki açılar ve kenar uzunlukları kullanılarak bulunur. Üçgenin tabanı, genellikle en uzun kenar olarak alınır. Yüksekliği ise, dik açı oluşturan kenarın uzantısı olarak bulunur. Üçgenin yüksekliği, Pivot Theorem ile de bulunabilir. Bu teorem, üçgenin bir köşesindeki açı ve kenar uzunluklarını kullanarak yüksekliği hesaplar.
Üçgenin Çeşitli Şekilleri Nasıl Hesaplanır?
Üçgenin çeşitleri, eşkenar üçgen, ikizkenar üçgen ve çeşitkenar üçgen olarak ayrılır. Eşkenar üçgende, tüm kenar uzunlukları eşittir. Ikizkenar üçgende, iki kenar uzunluğu eşittir. Çeşitkenar üçgende ise, tüm kenar uzunlukları farklıdır. Üçgenin çeşitleri, açılar ve kenar uzunlukları kullanılarak hesaplanabilir.
Üçgenin Alanı Nasıl Yuvarlanır?
Üçgenin alanı, genellikle yuvarlama işlemleri kullanılarak yuvarlanır. Üçgenin alanı, kesirli sayılar ile hesaplandığında, yuvarlama işlemi gerekir. Yuvarlama, genellikle ondalık sayılar kullanılarak yapılır. Üçgenin alanı, yuvarlama işleminden sonra, yaklaşık değer olarak bulunur. Bu yüzden, üçgenin alanı hesaplanırken, yuvarlama işlemleri dikkatli bir şekilde yapılmalıdır.