Bir Doğrunun Denklemi Nasıl Bulunur?

Matematikte bir doğrunun denklemi, o doğrunun üzerindeki tüm noktaların koordinatlarını belirten bir eşitliktir. Bu eşitlik, doğrunun konumunu ve yönünü tam olarak tanımlar. Bir doğrunun denklemi bulmak, geometri ve cebir konusundaki temel beceriler arasında yer alır. Doğrunun denklemi, çeşitli alanlarda, örneğin fizik, mühendislik ve bilgisayar bilimlerinde yaygın olarak kullanılır. Bu makalede, bir doğrunun denklemi nasıl bulunur, hangi adımlar takip edilir ve hangi yöntemler kullanılır, bunlara yanıt arayacağız.
Bir Doğrunun Denklemi Nasıl Bulunur?
Bir doğrunun denklemi, geometride bir noktadan geçen ve belli bir açıda bulunan bir doğrunun matematiksel ifadesidir. Bu denklem, doğrunun konumunu ve yönelimini belirlemek için kullanılır.
Doğrunun Eğim-Açı Katsayısı Yöntemi
Bu yöntemde, doğrunun eğim açı katsayısı (m) kullanılır. Eğim açı katsayısı, doğrunun y eksenine göre olan açısını belirler. Denklemi bulmak için, şu formül kullanılır: y = mx + b, burada m eğim açı katsayısı, b ise y eksenine göre olan kesme noktasıdır.
Uygunsuz Zamanlarda Gülme Nasıl Durdurulur?| Eğim Açı Katsayısı (m) | Kesme Noktası (b) | Denklem |
|---|---|---|
| 2 | 3 | y = 2x + 3 |
| -1 | 4 | y = -x + 4 |
| 0 | 5 | y = 5 |
Doğrunun İki Noktadan Geçme Yöntemi
Bu yöntemde, doğrunun iki noktadan geçmesi kullanılır. İki noktanın koordinatları bilinirse, doğrunun denklemi bulunabilir. İki noktanın koordinatları (x1, y1) ve (x2, y2) olsun. Denklemi bulmak için, şu formül kullanılır: y – y1 = (y2 – y1) / (x2 – x1) (x – x1).
Doğrunun Bir Nokta ve Eğiminden Bulma Yöntemi
Bu yöntemde, doğrunun bir nokta ve eğiminden yararlanılır. Bir noktanın koordinatları (x1, y1) ve eğim açı katsayısı (m) bilinirse, doğrunun denklemi bulunabilir. Denklemi bulmak için, şu formül kullanılır: y – y1 = m (x – x1).
Doğrunun İki Eğim Açısından Bulma Yöntemi
Bu yöntemde, iki doğrunun eğim açı katsayısı kullanılır. İki doğrunun eğim açı katsayısı (m1) ve (m2) olsun. İki doğrunun kesme noktası bilinirse, doğrunun denklemi bulunabilir. Denklemi bulmak için, şu formül kullanılır: y = (m1 x + b1) / (m2 x + b2).
Begonvil Nasıl Yetiştirilir?Doğrunun Grafikten Bulma Yöntemi
Bu yöntemde, doğrunun grafikten yararlanılır. Grafikte bir doğrunun konumunu ve yönelimini belirlemek için kullanılır. Grafikten doğrunun denklemi bulunabilir. Denklemi bulmak için, grafikteki iki noktanın koordinatları kullanılır.
Bir dogrunun denklemi nasıl bulunur?

Bir doğrunun denklemi, trục noktaları ve yönelimini kullanarak bulunur. Bu yöntem, doğrunun denklemi oluşturmak için kullanılır.
Doğrunun İki Noktayla Belirlenmesi
Doğrunun denklemi, iki nokta kullanılarak bulunur. Bu noktalar, doğrunun üzerinde bulunur ve (x₁, y₁) ve (x₂, y₂) olarak gösterilir. Doğrunun denklemi, aşağıdaki formülle bulunur:
- y – y₁ = (y₂ – y₁) / (x₂ – x₁) (x – x₁)
- y = mx + b, burada m = (y₂ – y₁) / (x₂ – x₁) ve b = y₁ – mx₁
yönelim, doğrunun eğimini gösterir.
Kâğıttan Turna Kuşu Nasıl Yapılır?Doğrunun Eğimli Noktayla Belirlenmesi
Doğrunun denklemi, bir nokta ve yönelim kullanılarak bulunur. Bu nokta, doğrunun üzerinde bulunur ve (x₀, y₀) olarak gösterilir. Doğrunun denklemi, aşağıdaki formülle bulunur:
- y – y₀ = m (x – x₀)
- y = mx + b, burada m = yönelim ve b = y₀ – mx₀
m, doğrunun yönelimini gösterir.
Doğrunun Normal Vektörüyle Belirlenmesi
Doğrunun denklemi, normal vektörü kullanılarak bulunur. Normal vektörü, doğrunun üzerindeki bir nokta ve yönelimine dik bir vektördür. Doğrunun denklemi, aşağıdaki formülle bulunur:
- ax + by + c = 0
- a = normal vektörünün x bileşeni
- b = normal vektörünün y bileşeni
- c = – (ax₀ + by₀)
a ve b, normal vektörünün bileşenlerini gösterir.
Doğrunun Parametrik Denklemi
Doğrunun parametrik denklemi, parametre t kullanılarak bulunur. Parametrik denklem, aşağıdaki formülle bulunur:
- x = x₀ + mt
- y = y₀ + nt
m ve n, doğrunun yönelimini gösterir.
Doğrunun Genel Denklemi
Doğrunun genel denklemi, Ax + By + C = 0 formülündedir. Burada A, B ve C, gerçek sayılar olup, doğrunun denklemi oluşturulur.
- A, B ve C, doğrunun denklemi oluşturulur
- Ax + By + C = 0, doğrunun genel denklemi
A, B ve C, doğrunun genel denklemi oluşturulur.
Bir doğrunun eğimi nasıl bulunur?

Bir doğrunun eğimi, o doğrunun dikCOORDINATE sisteminde slope-intercept formülünü kullanarak bulunur. Bu formül, y = mx + b şeklindedir, burada m eğimi, b ise y-kesimidir.
Doğrunun Eğimi Formülleri
Bir doğrunun eğimi, iki nokta arasındaki uzaklık ve bu noktalar arasındaki düşey uzaklığa bölünerek bulunur. Bu formül, m = (y2 – y1) / (x2 – x1) şeklindedir, burada (x1, y1) ve (x2, y2) iki noktadır.
Doğrunun Eğimi Çeşitleri
Bir doğrunun eğimi, pozitif, negatif veya sıfır olabilir. Pozitif eğimli bir doğrunun grafiği, yukarı doğru yönlendirirken, negatif eğimli bir doğrunun grafiği, aşağı doğru yönlendirir. Sıfır eğimli bir doğrunun grafiği ise, yatay bir çizgidir.
Doğrunun Eğimi Uygulamaları
Bir doğrunun eğimi, gerçek hayatta çeşitli uygulamaları vardır. Örneğin, bir şirketin gelirinin zamana göre değişimini göstermek için kullanılır. Ayrıca, bir nesnenin hareketini göstermek için de kullanılır.
Doğrunun Eğimi Hesaplama Yöntemleri
Bir doğrunun eğimi, çeşitli yöntemler kullanılarak hesaplanabilir. Bunlar arasında, slope-intercept formülünü kullanarak, iki nokta arasındaki uzaklık ve düşey uzaklığa bölünerek, veya grafik kullanarak eğimi hesaplamak yer alır.
- Slope-intercept formülünü kullanarak
- İki nokta arasındaki uzaklık ve düşey uzaklığa bölünerek
- Grafik kullanarak
Doğrunun Eğimi ile İlgili Kavramlar
Bir doğrunun eğimi ile ilgili kavramlar, y-kesimi, x-kesimi ve eğimin tersidir. Bunlar, bir doğrunun eğimi hesaplanırken kullanılır.
Iki doğrunun eğimi nasıl bulunur?
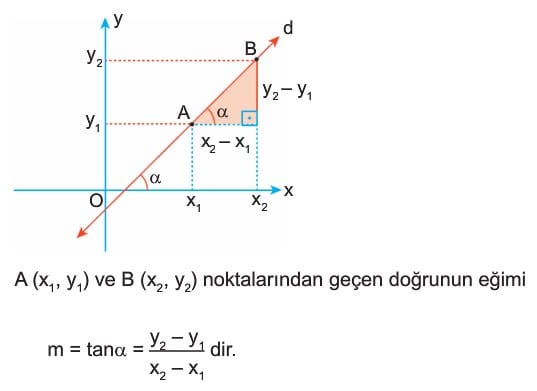
Iki doğrunun eğimi, iki doğrunun birbirine göre olan eğimidir. Birbirine göre olan eğimi bulmak için, iki doğrunun denklemlerini bilmemiz gerekir. İki doğrunun denklemleri şu şekilde verilir:
y = mx + b
Burada, m eğimin slope (eğim) olup, b ise y ekseni kesim noktasını gösterir.
Iki doğrunun eğimi bulunurken, iki doğrunun denklemlerini karşılaştırarak, slope (eğim) değerlerini buluyoruz. Eğer iki doğrunun slope (eğim) değerleri eşit ise, iki doğru paralel olup, eğimi yoktur. Eğer slope (eğim) değerleri farklı ise, iki doğru birbirine dik olup, eğimi vardır.
İki Doğrunun Eğiminin Formülleri
İki doğrunun eğiminin formülleri şu şekilde verilir:
m1 = (y2 – y1) / (x2 – x1)
m2 = (y4 – y3) / (x4 – x3)
Burada, m1 ve m2 iki doğrunun slope (eğim) değerleridir. Eğer m1 = m2 ise, iki doğru paralel olup, eğimi yoktur.
İki Doğrunun Eğiminin Çeşitleri
İki doğrunun eğiminin çeşitleri şu şekilde verilir:
- Paralel doğrunun eğimi: İki doğrunun slope (eğim) değerleri eşit ise, iki doğru paralel olup, eğimi yoktur.
- Dik doğrunun eğimi: İki doğrunun slope (eğim) değerleri farklı ise, iki doğru birbirine dik olup, eğimi vardır.
- Çakışık doğrunun eğimi: İki doğrunun slope (eğim) değerleri eşit ise, iki doğru çakışık olup, eğimi yoktur.
İki Doğrunun Eğiminin Uygulamaları
İki doğrunun eğiminin uygulamaları Şu şekilde verilir:
- Fizikte, iki doğrunun eğimi, kuvvetlerin bileşkesini bulmak için kullanılır.
- Mühendislikte, iki doğrunun eğimi, yapıların stabilize edilmesinde kullanılır.
- Coğrafyada, iki doğrunun eğimi, haritaların oluşturulmasında kullanılır.
İki Doğrunun Eğiminin Örnekleri
İki doğrunun eğiminin örnekleri şu şekilde verilir:
- y = 2x + 3 ve y = 2x – 4 doğrunun eğimi, paralel olup, eğimi yoktur.
- y = x + 2 ve y = 3x – 4 doğrunun eğimi, dik olup, eğimi vardır.
- y = 4x – 2 ve y = 4x + 3 doğrunun eğimi, çakışık olup, eğimi yoktur.
İki Doğrunun Eğiminin İleri Seviye Uygulamaları
İki doğrunun eğiminin ileri seviye uygulamaları şu şekilde verilir:
- Diferansiyel denklemlerde, iki doğrunun eğimi, çözümlerin bulunmasında kullanılır.
- Lineer cebirde, iki doğrunun eğimi, matrislerin çarpımında kullanılır.
- Kompleks analizde, iki doğrunun eğimi, fonksiyonların tayininde kullanılır.
Orijinden geçen doğrunun denklemi nedir?
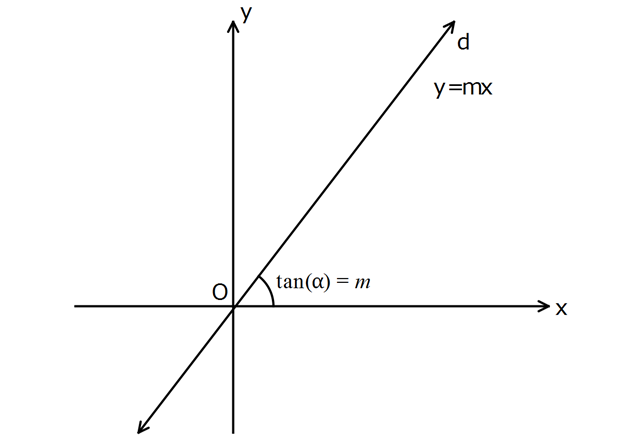
Orijinden geçen doğrunun denklemi, koordinat geometrisinde kullanılan bir matematiksel kavramdır. Bir doğru, orijindeki (0,0) noktasından geçen bir doğrudur. Bu doğrunun denklemi, y = mx şeklinde ifade edilir, burada m, doğrunun eğimidir.
Orijinden geçen doğrunun denklemi nasıl bulunur?
Orijinden geçen doğrunun denklemi, eğimi bilinen bir doğrunun denklemi olarak bulunur. Eğer eğimi m olan bir doğrunun denklemi y = mx olarak bilinirse, orijinden geçen doğrunun denklemi de y = mx olur.
Orijinden geçen doğrunun özellikleri nelerdir?
Orijinden geçen doğrunun bazı önemli özellikleri şunlardır:
- Orijinden geçen doğrunun denklemi her zaman y = mx şeklindedir.
- Doğrunun eğimi m, orijinden geçen doğrunun denklemini belirtilir.
- Orijinden geçen doğrunun grafiği, orijinden geçen bir çizgidir.
Orijinden geçen doğrunun uygulamaları nelerdir?
Orijinden geçen doğrunun uygulamaları şunlardır:
- Fizikte, orijinden geçen doğrunun denklemi, hareketli cisimlerin konumunu belirlemek için kullanılır.
- Mühendislikte, orijinden geçen doğrunun denklemi, yapı tasarımında kullanılır.
- Ekonomide, orijinden geçen doğrunun denklemi, talep ve arz eğrilerinin analizi için kullanılır.
Orijinden geçen doğrunun denklemi ile ilgili problemler nasıl çözülür?
Orijinden geçen doğrunun denklemi ile ilgili problemler, doğrunun denklemini kullanarak çözülür. Örneğin, orijinden geçen bir doğrunun denklemi y = 2x ise, bu doğrunun herhangi bir noktası (x,y) için y = 2x denklemine göre bulunur.
Daha fazla bilgi
Bir doğrunun denklemi nasıl bulunur?
Bir doğrunun denklemi, kordinat geometrisi sayesinde bulunur. İlk olarak, doğrunun eksen kesişimi ve eğimi bilinmelidir. Daha sonra, bu bilgiler kullanılarak doğrunun denklemi oluşturulur. Örneğin, bir doğrunun eksen kesişimi (a, b) noktasında ve eğimi m ise, doğrunun denklemi y = mx + (b – ma) şeklindedir.
Bir doğrunun denklemi ne türlü kullanılır?
Bir doğrunun denklemi, matematiksel modelleme ve problem çözme gibi alanlarda yaygın olarak kullanılır. Örneğin, bir fiziksel olay modellemek için bir doğrunun denklemi kullanılır. Ayrıca, bir doğrunun denklemi, istatistiksel analiz ve veri analizi gibi alanlarda da kullanılır. Bunun dışında, bir doğrunun denklemi, mühendislik ve ekonomi gibi alanlarda da kullanılır.
Bir doğrunun denklemi hangi alanlarda kullanılır?
Bir doğrunun denklemi, fizik, kimya, biyoloji, mühendislik, ekonomi ve istatistik gibi alanlarda yaygın olarak kullanılır. Ayrıca, bir doğrunun denklemi, bilgisayar bilimi ve veri analizi gibi alanlarda da kullanılır. Bunun dışında, bir doğrunun denklemi, matematiksel modelleme ve problem çözme gibi alanlarda da kullanılır.
Bir doğrunun denklemi nasıl uygulanır?
Bir doğrunun denklemi, pratik uygulamalar için kullanılır. Örneğin, bir mühendis, bir köprünün yüksekliğini ve uzunluğunu hesaplamak için bir doğrunun denklemi kullanılır. Ayrıca, bir istatistikçi, bir veri setinin trendini analiz etmek için bir doğrunun denklemi kullanılır. Bunun dışında, bir fizikçi, bir fiziksel olay modellemek için bir doğrunun denklemi kullanılır.