Bir Dairenin Çevresi Nasıl Hesaplanır?

Bir dairenin çevresi, özellikle matematik ve geometri derslerinde sık sık karşılaşılan bir kavramdır. Çevre, dairenin sınırını oluşturan noktalardan geçen hayali çizginin uzunluğudur. Çevrenin hesabında ise, π (pi) sayısı ve dairenin yarıçapı kullanılır. Bir dairenin çevresi nasıl hesaplanır sorusunun cevabı, geometrik hesaplamalarda ve gerçek hayatın çeşitli alanlarında önemli bir yere sahiptir. Bu yüzden, bu makalede bir dairenin çevresi nasıl hesaplanır, bu hesabın hangi formülle yapıldığı ve günlük hayatımızda bu hesabın hangi alanlarında kullanıldığı anlatılacaktır.

Bir Dairenin Çevresi Nasıl Hesaplanır?

Çevre, bir dairenin etrafını çevreleyen mesafeye verilen isimdir. Çevrenin hesaplanması için, dairenin yarıçapı veya çapına ihtiyaç duyulur. Aşağıda, çevrenin hesaplanmasına yardımcı olacak formüller ve adımlar yer almaktadır.

Çevre Formülü

Çevre formülü, π (pi sayısı) ve yarıçapın (r) çarpımına eşittir: C = 2 × π × r. Burada, C çevrenin uzunluğunu, π pi sayısı (yaklaşık 3,14) ve r yarıçapın uzunluğunu temsil etmektedir.

Çap Kullanarak Çevre Hesaplaması

Çapı bilinen bir dairenin çevresi, çapın π sayısıyla çarpımına eşittir: C = π × d. Burada, C çevrenin uzunluğunu, π pi sayısı ve d çapın uzunluğunu temsil etmektedir.

Çevre Hesaplamak için Örnek

Örnek: Bir dairenin yarıçapı 4 cm ise, çevresi şu şekilde hesaplanır:

1. C = 2 × π × 4
2. C = 2 × 3,14 × 4
3. C = 25,12 cm

Çevre Hesaplamasında Kullanılan Birimler

Çevre hesaplamasında kullanılan birimler, genellikle santimetre (cm), metre (m) veya kilometre (km) gibi uzunluk birimlerinden oluşur.

Çevre Hesaplamasının Önemi

Çevre hesaplamasının önemi, günlük hayatımızda karşılaşabileceğimiz birçok sorunu çözmemize yardımcı olur. Örneğin, bir dairenin çevresini hesaplamak, bir bina inşa etmek için gerekli olan malzeme miktarını belirlemek için kullanılır.

Dairenin çevresi nasıl hesaplanır?

Dairenin çevresi, yarıçapının iki katı ile π (pi) sayısının çarpımına eşittir. Matematiksel olarak, bu formülle ifade edilir: C = 2 × π × r, burada C, dairenin çevresi ve r, yarıçapını temsil eder.

Dairenin Çevresini Hesaplamak için Gerekli Bilgiler

Dairenin çevresi hesaplamak için, yarıçapının veya çapının bilinmesi gerekir. Çap, dairenin merkez noktasından geçen ve dairenin kenarına dokunan bir doğru parçasıdır. Yarıçap, çapın yarısıdır.

Dairenin Çevresinin Formülü

Dairenin çevresi formülü, C = 2 × π × r, burada:

1. C, dairenin çevresi
2. π, pi sayısı (yaklaşık 3,14)
3. r, yarıçap

Dairenin Çevresini Hesaplamak için Örnek

Örnek: Bir dairenin yarıçapı 4 cm ise, çevresi nasıl hesaplanır?

1. C = 2 × π × r
2. C = 2 × 3,14 × 4
3. C = 25,12 cm

Dairenin Çevresinin Önemi

Dairenin çevresi, günlük yaşamda birçok alanda kullanılır. Örneğin, inşaat mühendisliğinde, dairenin çevresi, bina çevresinin hesaplanmasında kullanılır. Ayrıca, fizik ve mühendislik alanlarında dairenin çevresi, kuvvet ve momentum hesaplamalarında kullanılır.

Dairenin Çevresini Hesaplamak için İpuçları

Dairenin çevresi hesaplamak için, yarıçapının doğru bir şekilde ölçülmesi gerekir. Ayrıca, π sayısı, yaklaşık olarak 3,14 olarak alınır. Dikkatli hesaplama, dairenin çevresi hesaplamasında önemlidir.

Çemberin çevresi nasıl hesaplanır örnek?

Çemberin çevresi, yarıçapı bilinen bir çemberin çevresini hesaplamak için kullanılan bir formüldür. Bu formül, çemberin yarıçapını ikiyle çarparak çevresini elde eder. Formül şu şekilde ifade edilir: Çevre = 2 × π × yarıçap.

Çemberin Çevresi Formülü

Çemberin çevresi formülü, matematikteki en temel formüllerden biridir. Bu formül, çemberin yarıçapını ikiyle çarparak çevresini elde eder. Formül şu şekilde ifade edilir: Çevre = 2 × π × yarıçap.

Çemberin Çevresi Hesaplamak için Gerekli Bilgiler

Çemberin çevresi hesaplamak için gereken bilgiler şunlardır:

1. Yarıçap: Çemberin yarıçapı, çemberin merkez noktasından bir noktaya olan uzaklıktır.
2. Çemberin Merkezi: Çemberin merkezi, çemberin merkez noktasıdır.
3. Çemberin Çevresi: Çemberin çevresi, çemberin çevre uzunluğudur.

Çemberin Çevresi Hesaplamak için Uygulama

Çemberin çevresi hesaplamak için uygulamada şu adımlar takip edilir:

1. Çemberin yarıçapını belirleyin.
2. Çemberin yarıçapını ikiyle çarpın.
3. Çemberin çevresi hesaplamak için π sayısını çarpın.
4. Çemberin çevresi hesaplanmıştır.

Çemberin Çevresi Hesaplamak için Örnek

Örnek: Çemberin yarıçapı 4 cm ise, çemberin çevresi nasıl hesaplanır?

1. Çemberin yarıçapı 4 cm ise, yarıçapını ikiyle çarpın: 2 × 4 = 8.
2. Çemberin çevresi hesaplamak için π sayısını çarpın: 8 × π = 25.13 cm.
3. Çemberin çevresi hesaplanmıştır: 25.13 cm.

Çemberin Çevresi Hesaplamak için Faydaları

Çemberin çevresi hesaplamak için faydaları şunlardır:

1. Dairenin Çevresi: Çemberin çevresi, dairenin çevresini hesaplamak için kullanılır.
2. Çemberin Alanı: Çemberin çevresi, çemberin alanını hesaplamak için kullanılır.
3. Matematik Problemlerinde: Çemberin çevresi, matematik problemlerinde kullanılır.

7 sınıf dairenin çevresi nasıl bulunur?

Dairenin Çevresini Bulma

Dairenin çevresi, yarıçapın iki katı ile π sayısının çarpımına eşittir. Matematiksel olarak, bu formülle gösterilir: C = 2 × π × r, burada C dairenin çevresi, r yarıçapıdır.

Dairenin Çevresini Bulmak İçin Gerekli Bilgiler

Dairenin çevresi bulunabilmesi için yarıçapın bilinmesi gerekir. Yarıçap yoksa, çapın yarısı alınarak yarıçap bulunur. Dairenin merkezinden geçen bir çap, dairenin yarıçapına eşit uzunluktadır.

Dairenin Çevresini Bulma Formülü

Dairenin çevresi, yarıçapın iki katı ile π sayısının çarpımına eşittir. Bu formül, dairenin çevresi bulunmasında kullanılır.

1. C = 2 × π × r
2. C: Dairenin çevresi
3. r: Yarıçap
4. π: π sayısı (3,14)

Dairenin Çevresini Bulma Örnekleri

Dairenin çevresi bulunmasında, yarıçapın bilinmesi gerekir. Aşağıdaki örneklerde, yarıçap verilmiş ve dairenin çevresi bulunmuştur.

1. r = 4 cm ise, C = 2 × π × 4 = 25,12 cm
2. r = 6 cm ise, C = 2 × π × 6 = 37,68 cm
3. r = 8 cm ise, C = 2 × π × 8 = 50,24 cm

Dairenin Çevresini Bulmada Kullanılan Kavramlar

Dairenin çevresi bulunmasında, aşağıdaki kavramlar kullanılır:

1. Çap: Dairenin merkezinden geçen bir çizgi
2. Yarıçap: Çapın yarısı
3. Çevre: Dairenin çevre uzunluğu
4. π sayısı: 3,14 olan matematiksel bir sayı

Dairenin alanı nasıl bulunur örnek?

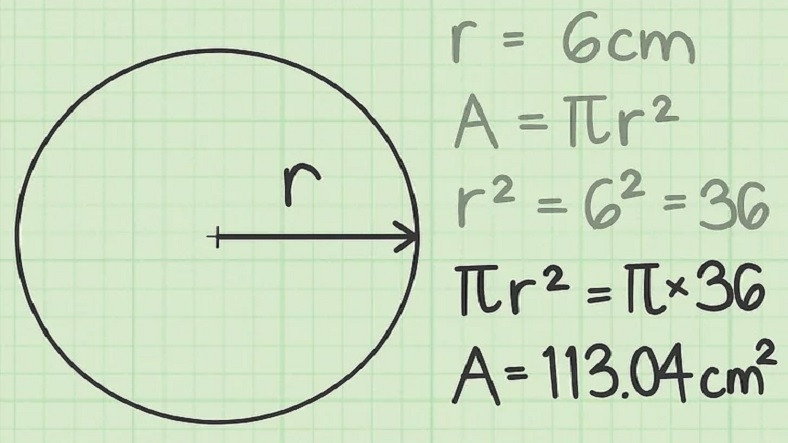
Dairenin alanı, yarıçapı (r) ve pi (π) sayıları kullanılarak bulunur. Formül şu şekildedir: Alan = π × r². Örneğin, yarıçapı 4 cm olan bir dairenin alanı şöyle bulunur: Alan = π × 4² = 3,14 × 16 = 50,24 cm².

Dairenin Çevresi Nasıl Bulunur?

Dairenin çevresi, yarıçapı (r) ve pi (π) sayıları kullanılarak bulunur. Formül şu şekildedir: Çevre = 2 × π × r. Örneğin, yarıçapı 4 cm olan bir dairenin çevresi şöyle bulunur: Çevre = 2 × 3,14 × 4 = 25,12 cm.

Dairenin Merkezi Nasıl Bulunur?

Dairenin merkezi, dairenin simetri merkezi olarak tanımlanır. Merkezi bulmak için, dairenin iki çap noktasının orta noktasını bulmak gerekir. Örneğin, bir dairenin çap noktaları A ve B ise, merkezi şu şekilde bulunur: Merkez = (A + B) / 2.

Dairenin Yarıçapı Nasıl Bulunur?

Dairenin yarıçapı, dairenin merkez noktasından herhangi bir noktasına olan uzaklıktır. Yarıçapı bulmak için, dairenin çevresi ve pi (π) sayısı kullanılır. Formül şu şekildedir: r = Çevre / (2 × π). Örneğin, çevresi 25,12 cm olan bir dairenin yarıçapı şöyle bulunur: r = 25,12 / (2 × 3,14) = 4 cm.

Dairenin Özellikleri Nelerdir?

Dairenin özellikleri şunlardır:

1. Simetri merkezi vardır.
2. Çapı yarıçapın iki katıdır.
3. Çevresi pi (π) sayısı kullanılarak bulunur.
4. Alanı pi (π) sayısı ve yarıçapı kullanılarak bulunur.
5. İç açıları toplamı 360 derecedir.

Daha fazla bilgi

Bir dairenin çevresi nasıl hesaplanır?

Bir dairenin çevresi, yarıçapı veya çapı bilinen bir dairenin çevresini hesaplamak için kullanılan bir formül vardır. Bu formül, π (pi) sayısı ile yarıçapın çarpımına eşitlenir. Yani, bir dairenin çevresi, π sayısı ile yarıçapın çarpımına eşitlenir. π sayısı, yaklaşık olarak 3,14 olarak kabul edilir. Örneğin, yarıçapı 4 cm olan bir dairenin çevresi, π sayısı ile 4 cm’nin çarpımına eşitlenir. Yani, çevre yaklaşık olarak 16,56 cm’dir.

Çevre hesabı için hangi değerler gerekir?

Çevre hesabı için, yarıçap veya çap değerine ihtiyaç vardır. Bu değerler, dairenin boyutunu belirlemek için kullanılır. Eğer yarıçapı bilinmiyorsa, çapı bilinirse, yarıçapı kolayca hesaplanabilir. Çapı, dairenin çapına eşit olan uzunluğudur. Yarıçapı ise, çapı ikiye bölünmüş olan uzunluğudur. Örneğin, çapın 8 cm olduğu bir dairenin yarıçapı, 8 cm’nin yarısı olan 4 cm’dir.

Bir dairenin çevresini hesaplamak için formül nedir?

Bir dairenin çevresini hesaplamak için kullanılan formül, C = 2 × π × r şeklindedir. Burada, C, çevreyi; π, pi sayısını; ve r, yarıçapı temsil eder. Bu formül, bir dairenin çevresini hesaplamak için kullanılır. Örneğin, yarıçapı 5 cm olan bir dairenin çevresi, C = 2 × π × 5 formülünü kullanarak hesaplanabilir. Burada, π sayısı yaklaşık olarak 3,14 olarak kabul edilir. Yani, çevre yaklaşık olarak 31,4 cm’dir.

Çevre hesaplamasında hangi hata yapılabilir?

Çevre hesaplamasında en yaygın hata, yarıçap veya çap değerinin yanlış hesaplanmasıdır. Yarıçap veya çap değerinin yanlış hesaplanması, çevre hesaplamasında büyük hatalara yol açabilir. Örneğin, yarıçapı 3 cm olan bir dairenin çevresi hesaplanırken, yarıçapı 4 cm olarak yanlış hesaplanırsa, çevre hesaplamasında büyük bir hata olacaktır. Bu yüzden, yarıçap veya çap değerinin doğru hesaplanması çok önemlidir.